Binary Search Algorithm
Binary search is an algorithm used for searching for elements in a way that halves the possible elements every time it guesses. This is very efficient, especially when the number of elements to search through is very high.
A friend presents you with an array of twenty ordered numbers, saying she has chosen one as her lucky number and that you must guess what it is. She will only tell you if the number is higher or lower than your guess each time. You could choose a random number each time, based upon her answers, but this would be quite inefficient. You could also start at the first number, guessing each one consecutively until the correct number is reached (this is called linear search). This also could take a long time to guess the correct number. What if there were 400 numbers! The worst case would be 400 guesses - very tiring!
The best way to find the correct number is by using binary search. This means picking the middle position each time you guess. By doing this, you split the possibilities in half. Your friend will tell you whether her lucky number is higher or lower than your guess, and now you can discount all of the numbers that are no longer needed. Below is a gif to explain how it works (from penjee.com).
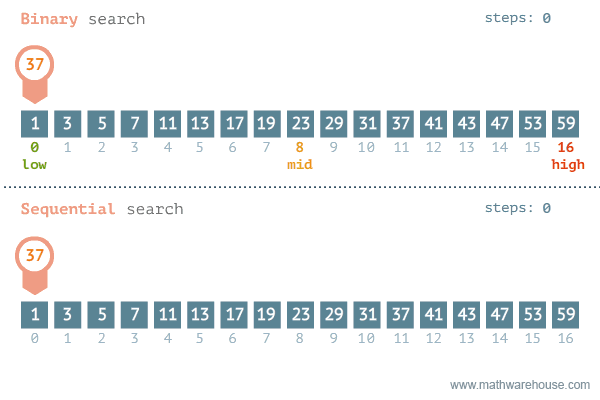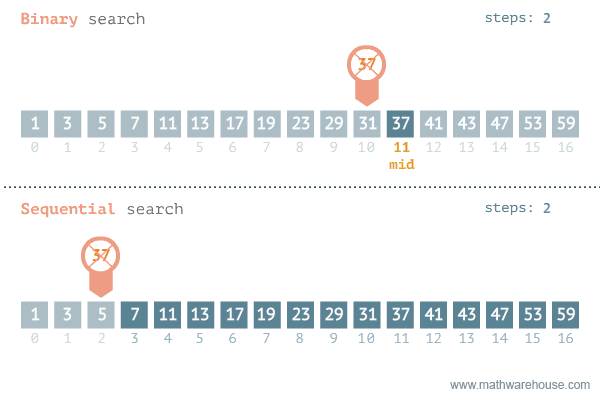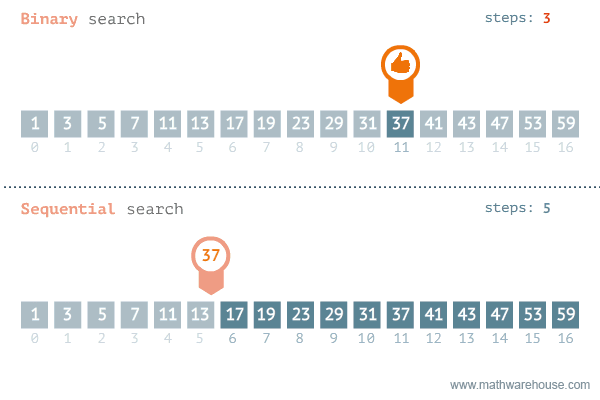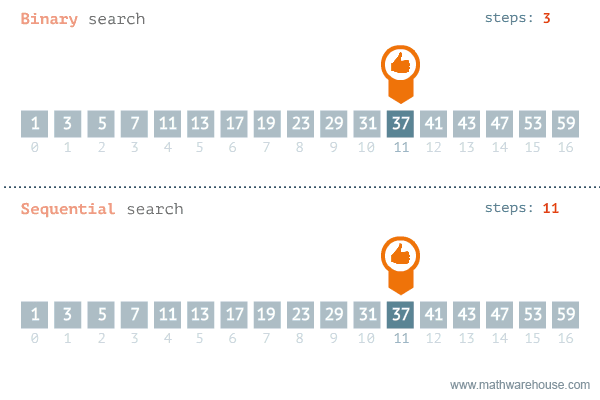
Because the possibilities are divided by two with each guess, you will also notice that if our friend were to double the range of numbers to choose from the next time around, the number of times we would have to guess only increases by one. This makes binary search immensely more efficient than linear search.
Calculating the Amount of Guesses Needed, Using Logarithms
The binary search we repeatedly halve the amount of possibilities until we reach the possibility that is correct. If we know the number of possibilities, how can we calculate the number of times we will need to guess? Using a base-two logarithm of the number of possibilites we can easily find out.
A logarithm is used in algebra to figure out what n equals, when 6^n = 216. To write this equation as a logarithm it looks like this:

We are asking, “Six to the power of what equals two hundred and sixteen?”. The equation above could also be solved by multiplying six by itself repeatedly until it reaches 216, then counting the amount of times that we multiplied. In this case it is 3 times, 6^3 = 216.
For the binary search algorithm, we use a logarithm with a base of two, because we are always splitting our possible range into two parts. For instance, if there are 600 sorted possibilities, we are asking, “Two to the power of what equals 600?”. Our logarithm looks like this:

Let’s work it out. If we multiply 2 by itself 9 times we reach 512, and 10 times we reach 1024, so if we have 600 possibilities it should take us between 9 and 10 guesses only to find the lucky number.